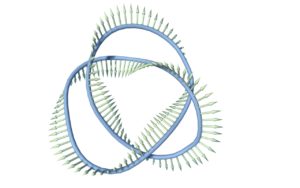
Visually, this can be pictured as a tangled ribbon with its two ends glued flat together, in such a way that the ribbon is an orientable surface. Note that this simply means we exclude cases in which the ribbon is glued together after an odd number of half-twists, such as a Mobius band. See the following Figure.

Two framings are considered to be equivalent if one can be transformed to another by
a smooth deformation. This is in fact an equivalence relation, and we will use the word
“framing” to refer to either an equivalence class or a representative vector field. It should
be clear from context which definition is being used. Similarly, a framed link in S^3 is a finite collection of framed knots that do not intersect. Throughout this document, the word “knot” will be used interchangeably with “link component” unless otherwise stated.
Given a framed knot (K,V ), we can construct a ribbon by pushing the knot K along the
vector field V . Conversely, given a closed ribbon in S^3 , we can construct a framed knot K
in the obvious way, by choosing the vector field to lie in the ribbon, and perpendicular to K
at every point of the knot. See the following Figure.

Given a knot, there are many distinct framings we can choose. Suppose that we are given a knot with a fixed framing. Since the vector field is smooth, there is some neighborhood on the knot (i.e., an interval) on which both the knot and vector field can be considered to lie in a plane. We obtain a new framing by replacing the portion of the vector field lying on this neighborhood with one that twists an integer multiple of 2π around the knot as it moves along the neighborhood. Intuitively, it seems clear that this is the only way, up to the equivalence relation for framed knots, to obtain a new framing from an old one, leaving the knot fixed.
This movie shows the Trefoil with three different framings.
See the article here for more details about framed knots.